Aller au contenu principal

Labyrinthe

Dans cette Situation d'Apprentissage et d'Évaluation, vous allez devoir implémenter des algorithmes de génération et de résolution de labyrinthes.

Préambule​

Notes sur l'organisation et l'évaluation​

  • Le projet est à réaliser en binômes.
  • Vous devez versionner votre travail avec git.
  • Le dépôt distant sera sur l'instance Gitlab du département informatique de l'IUT de Reims : https://iut-info.univ-reims.fr/gitlab/.
  • Il faut effectuer des commits réguliers (à chaque fois que vous travaillez sur votre projet et a minima pour chaque fonction/question).
  • Un entretien oral avec votre enseignant référent permettra de vous aider à réaliser votre projet et vous permettra de vous entraîner.
  • Il est déconseillé d'inclure dans votre notebook et dans votre dépôt, des solutions que vous n'auriez pas trouvées vous-même, ou que vous n'auriez pas comprises.

L'essentiel du travail est donc à réaliser dans un notebooks jupyter. Vous pouvez utiliser l'instancejupyterhub du département.

Consignes​

  • Votre code devra respecter quelques règles d'hygiène élémentaire :

    • contenir des commentaires (a minima un docstring informatif pour chaque méthode),
    • être lisible (en essayant d'utiliser des noms de variables explicites).

  • Respectez la progression du sujet dans la présentation de votre notebook.

  • Le travail est à réaliser en binôme Chaque membre du binôme doit être capable de répondre seul à des questions portant sur ce qui a été réalisé.

Modélisation d'un labyrinthe​

Un labyrinthe est un graphe non-orienté (ou orienté-symétrique) dont la représentation planaire prend la forme d'une grille. Chaque cellule du labyrinthe est un sommet du graphe, et l'absence de mur entre deux cellules contiguës constitue une arête.

On parle de labyrinthe parfait lorsque le graphe est un arbre (donc connexe et sans cycle). Par la suite, sauf mention du contraire, un labyrinthe sera considéré comme parfait.

Représentation d'un graphe parfait sous forme d'un arbre

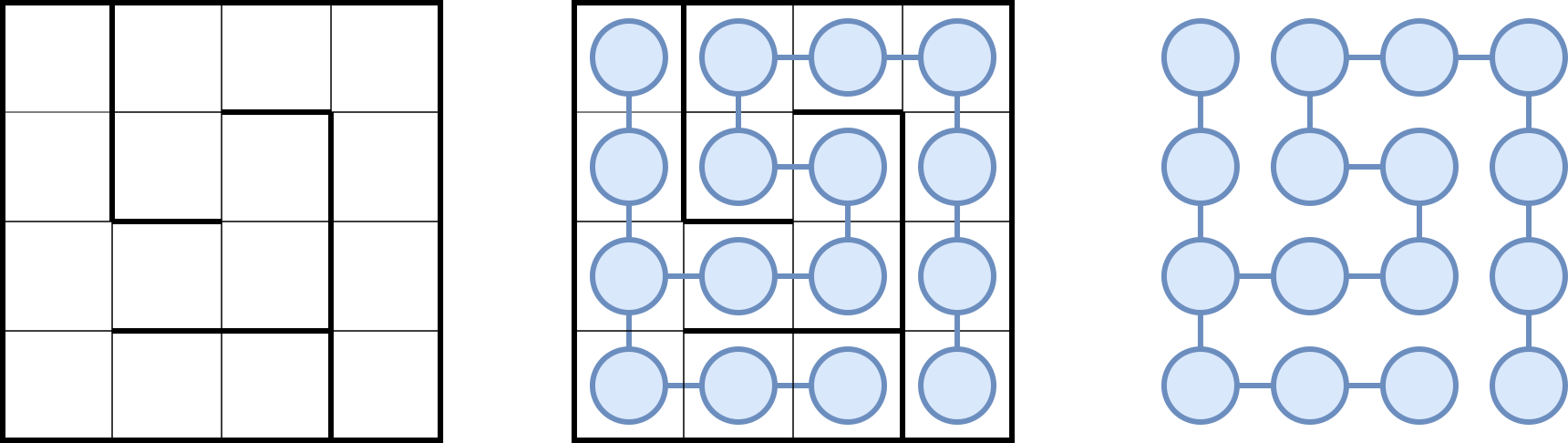
Arbre binaire

La modélisation retenue dans ce projet consiste à représenter un sommet par un couple (indice de ligne, indice de colonne) permettant de localiser la cellule, et d'utiliser un dictionnaire pour lister les voisines d'une cellule (et donc les arêtes).

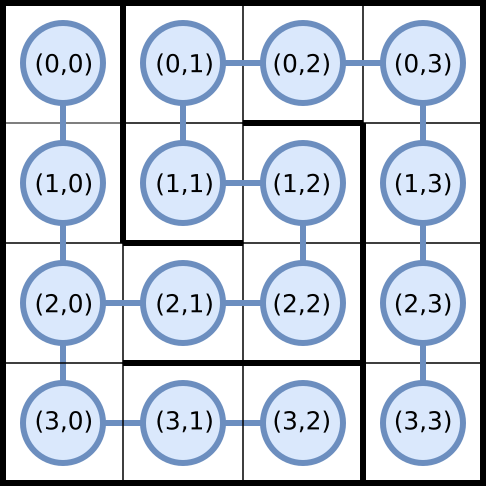
Arbre binaire

Arbre d'un graphe parfait avec sommets-coordonnées. Les voisins du sommet (2,0) sont (1,0), (2,1) et (3,0). Ceux du sommet (2,1) sont (2,0) et (2,2).

Dans l'exemple précédent, les sommets du graphe sont les cellules :

(0, 0), (0, 1), (0, 2), (0, 3), (1, 0), (1, 1), (1, 2), (1, 3), (2, 0), (2, 1), (2, 2), (2, 3), (3, 0), (3, 1), (3, 2), (3, 3)

Les arêtes sont :

{(0, 0), (1, 0)}, {(1, 0), (2, 0)}, {(2, 0), (3, 0)}, {(2, 0), (2, 1)}, ...

Les voisinages (les successeurs, en quelque sorte) correspondants :

{
    (0, 0): {(1, 0)}, 
    (0, 1): {(0, 2), (1, 1)}, 
    (0, 2): {(0, 1), (0, 3)}, 
    (0, 3): {(0, 2), (1, 3)}, 
    (1, 0): {(2, 0), (0, 0)}, 
    (1, 1): {(0, 1), (1, 2)}, 
    (1, 2): {(1, 1), (2, 2)}, 
    (1, 3): {(2, 3), (0, 3)}, 
    (2, 0): {(1, 0), (2, 1), (3, 0)}, 
    (2, 1): {(2, 0), (2, 2)}, 
    (2, 2): {(1, 2), (2, 1)}, 
    (2, 3): {(3, 3), (1, 3)}, 
    (3, 0): {(3, 1), (2, 0)}, 
    (3, 1): {(3, 2), (3, 0)}, 
    (3, 2): {(3, 1)}, 
    (3, 3): {(2, 3)}
}

Implémentation​

Nous allons définir la classe Maze à l'aide des attributs :

  • height, le nombre de lignes (int) de la grille du labyrinthe (autrement dit, la hauteur, en nombre de cellules),
  • width, le nombre de colonnes (int) de la grille du labyrinthe (autrement dit, la hauteur, en nombre de cellules),
  • neighbors : un dictionnaire (dict) qui associe à chaque cellule, un set contenant ses voisins (c'est-à-dire les cellules qu'on peut atteindre en un déplacement, sans être bloqué par un mur).

Voici donc la définition sommaire de la classe Maze, pour laquelle nous vous fournissons, un constructeur par défaut, une méthode d'affichage (en ASCII), et une méthode qui résume les infos du labyrinthe :

"""
Classe Labyrinthe
Représentation sous forme de graphe non-orienté
dont chaque sommet est une cellule (un tuple (l,c))
et dont la structure est représentée par un dictionnaire
  - clés : sommets
  - valeurs : ensemble des sommets voisins accessibles
"""
class Maze:
    def __init__(self, height, width):
        """
        Constructeur d'un labyrinthe de height cellules de haut 
        et de width cellules de large 
        Les voisinages sont initialisés à des ensembles vides
        Remarque : dans le labyrinthe créé, chaque cellule est complètement emmurée
        """
    self.height = height
    self.width = width
    self.neighbors = {(i,j): set() for i in range(height) for j in range (width)}

    def info(self):
        """
        **NE PAS MODIFIER CETTE MÉTHODE**
        Affichage des attributs d'un objet 'Maze' (fonction utile pour deboguer)
        Retour:
            chaîne (string): description textuelle des attributs de l'objet
        """
        txt = "**Informations sur le labyrinthe**\n"
        txt += f"- Dimensions de la grille : {self.height} x {self.width}\n"
        txt += "- Voisinages :\n"
        txt += str(self.neighbors)+"\n"
        valid = True
        for c1 in {(i, j) for i in range(self.height) for j in range(self.width)}:
            for c2 in self.neighbors[c1]:
                if c1 not in self.neighbors[c2]:
                    valid = False
                    break
            else:
                continue
            break
        txt += "- Structure cohérente\n" if valid else f"- Structure incohérente : {c1} X {c2}\n"
        return txt

    def __str__(self):
        """
        **NE PAS MODIFIER CETTE MÉTHODE**
        Représentation textuelle d'un objet Maze (en utilisant des caractères ascii)
        Retour:
            chaîne (str) : chaîne de caractères représentant le labyrinthe
        """
        txt = ""
        # Première ligne
        txt += "┏"
        for j in range(self.width-1):
            txt += "━━━┳"
        txt += "━━━┓\n"
        txt += "┃"
        for j in range(self.width-1):
            txt += "   ┃" if (0,j+1) not in self.neighbors[(0,j)] else "    "
        txt += "   ┃\n"
        # Lignes normales
        for i in range(self.height-1):
            txt += "┣"
            for j in range(self.width-1):
                txt += "━━━╋" if (i+1,j) not in self.neighbors[(i,j)] else "   ╋"
            txt += "━━━┫\n" if (i+1,self.width-1) not in self.neighbors[(i,self.width-1)] else "   ┫\n"
            txt += "┃"
            for j in range(self.width):
                txt += "   ┃" if (i+1,j+1) not in self.neighbors[(i+1,j)] else "    "
            txt += "\n"
        # Bas du tableau
        txt += "┗"
        for i in range(self.width-1):
            txt += "━━━┻"
        txt += "━━━┛\n"
        return txt

Exemples d'utilisation :

laby = Maze(4, 4)
print(laby.info())
**Informations sur le labyrinthe**
    - Dimensions de la grille : 4 x 4
    - Voisinages :
    {(0, 0): set(), (0, 1): set(), (0, 2): set(), (0, 3): set(), (1, 0): set(), (1, 1): set(), (1, 2): set(), (1, 3): set(), (2, 0): set(), (2, 1): set(), (2, 2): set(), (2, 3): set(), (3, 0): set(), (3, 1): set(), (3, 2): set(), (3, 3): set()}
    - Structure cohérente

    ┏━━━┳━━━┳━━━┳━━━┓
    ┃   ┃   ┃   ┃   ┃
    ┣━━━╋━━━╋━━━╋━━━┫
    ┃   ┃   ┃   ┃   ┃
    ┣━━━╋━━━╋━━━╋━━━┫
    ┃   ┃   ┃   ┃   ┃
    ┣━━━╋━━━╋━━━╋━━━┫
    ┃   ┃   ┃   ┃   ┃
    ┗━━━┻━━━┻━━━┻━━━┛

Cassons quelques murs en redéfinissant manuellement les voisinages des cellules concernées :

laby.neighbors = {
    (0, 0): {(1, 0)},
    (0, 1): {(0, 2), (1, 1)},
    (0, 2): {(0, 1), (0, 3)},
    (0, 3): {(0, 2), (1, 3)},
    (1, 0): {(2, 0), (0, 0)},
    (1, 1): {(0, 1), (1, 2)},
    (1, 2): {(1, 1), (2, 2)},
    (1, 3): {(2, 3), (0, 3)},
    (2, 0): {(1, 0), (2, 1), (3, 0)},
    (2, 1): {(2, 0), (2, 2)},
    (2, 2): {(1, 2), (2, 1)},
    (2, 3): {(3, 3), (1, 3)},
    (3, 0): {(3, 1), (2, 0)},
    (3, 1): {(3, 2), (3, 0)},
    (3, 2): {(3, 1)},
    (3, 3): {(2, 3)}
}

print(laby)
    ┏━━━┳━━━┳━━━┳━━━┓
    ┃   ┃           ┃
    ┣   ╋   ╋━━━╋   ┫
    ┃   ┃       ┃   ┃
    ┣   ╋━━━╋   ╋   ┫
    ┃           ┃   ┃
    ┣   ╋━━━╋━━━╋   ┫
    ┃           ┃   ┃
    ┗━━━┻━━━┻━━━┻━━━┛

Ajoutons maintenant un murs entre la cellule (1,3) et la cellule (2,3) que nous venons de retirer (autrement dit : supprimons une arête que nous avons ajoutée juste avant) :

laby.neighbors[(1,3)].remove((2,3))
laby.neighbors[(2,3)].remove((1,3))
print(laby)
    ┏━━━┳━━━┳━━━┳━━━┓
    ┃   ┃           ┃
    ┣   ╋   ╋━━━╋   ┫
    ┃   ┃       ┃   ┃
    ┣   ╋━━━╋   ╋━━━┫
    ┃           ┃   ┃
    ┣   ╋━━━╋━━━╋   ┫
    ┃           ┃   ┃
    ┗━━━┻━━━┻━━━┻━━━┛

et cassons-le :

laby.neighbors[(1,3)].add((2, 3))
laby.neighbors[(2,3)].add((1, 3))
print(laby)
    ┏━━━┳━━━┳━━━┳━━━┓
    ┃   ┃           ┃
    ┣   ╋   ╋━━━╋   ┫
    ┃   ┃       ┃   ┃
    ┣   ╋━━━╋   ╋   ┫
    ┃           ┃   ┃
    ┣   ╋━━━╋━━━╋   ┫
    ┃           ┃   ┃
    ┗━━━┻━━━┻━━━┻━━━┛
Attention

Comme vous pouvez le constater dans l'exemple qui précède :

Ajouter un mur entre une cellule c1 et une cellule c2 revient à diminuer deux voisinages, d'une cellule chacun ; il faut retirer c1 du voisinage de c2 et retirer c2 du voisinage de c1.

Casser un mur entre une cellule c1 et une cellule c2 revient à augmenter deux voisinages ; il faut ajouter c1 au voisinage de c2 et ajouter c2 au voisinage de c1.

La méthode info() fournie teste la cohérence des voisinages en vérifiant que, dès lors qu'une cellule c1 est dans le voisinage d'une cellule c2, alors c2 est aussi dans le voisinage de c1.

Dans l'exemple qui suit, un mur est ajouté entre (1,3) et (2,3). Si on a bien retiré (2,3) des voisins de (1,3) on a oublié de retirer (1,3) des voisins de (2,3).

On constate que le labyrinthe est visiblement bon, toutefois, la méthode info() détecte l'incohérence entre les cellules concernées.

laby.neighbors[(1, 3)].remove((2, 3))
print(laby)
print(laby.info())
    ┏━━━┳━━━┳━━━┳━━━┓
    ┃   ┃           ┃
    ┣   ╋   ╋━━━╋   ┫
    ┃   ┃       ┃   ┃
    ┣   ╋━━━╋   ╋━━━┫
    ┃           ┃   ┃
    ┣   ╋━━━╋━━━╋   ┫
    ┃           ┃   ┃
    ┗━━━┻━━━┻━━━┻━━━┛

    **Informations sur le labyrinthe**
    - Dimensions de la grille : 4 x 4
    - Voisinages :
    {(0, 0): {(1, 0)}, (0, 1): {(1, 1), (0, 2)}, (0, 2): {(0, 1), (0, 3)}, (0, 3): {(0, 2), (1, 3)}, (1, 0): {(2, 0), (0, 0)}, (1, 1): {(0, 1), (1, 2)}, (1, 2): {(1, 1), (2, 2)}, (1, 3): {(0, 3)}, (2, 0): {(1, 0), (2, 1), (3, 0)}, (2, 1): {(2, 0), (2, 2)}, (2, 2): {(1, 2), (2, 1)}, (2, 3): {(3, 3), (1, 3)}, (3, 0): {(3, 1), (2, 0)}, (3, 1): {(3, 2), (3, 0)}, (3, 2): {(3, 1)}, (3, 3): {(2, 3)}}
    - Structure incohérente : (2, 3) X (1, 3)

Corrigeons ça :

laby.neighbors[(2, 3)].remove((1, 3))

Testons maintenant s'il y a un mur entre deux cellules :

c1 = (1, 3)
c2 = (2, 3)
if c1 in laby.neighbors[c2] and c2 in laby.neighbors[c1]:
    print(f"Il n'y a pas de mur entre {c1} et {c2} car elles sont mutuellement voisines")
elif c1 not in laby.neighbors[c2] and c2 not in laby.neighbors[c1]:
    print(f"Il y a un mur entre {c1} et {c2} car {c1} n'est pas dans le voisinage de {c2} et {c2} n'est pas dans le voisinage de {c1}")
else:
    print(f"Il y a une incohérence de réciprocité des voisinages de {c1} et {c2}")
Il y a un mur entre (1, 3) et (2, 3) car (1, 3) n'est pas dans le voisinage de (2, 3) et (2, 3) n'est pas dans le voisinage de (1, 3)

Le même code permet de tester si on peut accéder à une cellule depuis l'autre et vice-versa :

c1 = (1, 3)
c2 = (2, 3)
if c1 in laby.neighbors[c2] and c2 in laby.neighbors[c1]:
    print(f"{c1} est accessible depuis {c2} et vice-versa")
elif c1 not in laby.neighbors[c2] and c2 not in laby.neighbors[c1]:
    print(f"{c1} n'est pas accessible depuis {c2} et vice-versa")
else:
    print(f"Il y a une incohérence de réciprocité des voisinages de {c1} et {c2}")
(1, 3) n'est pas accessible depuis (2, 3) et vice-versa

Parcourons maintenant la grille du labyrinthe pour lister l'ensemble des cellules :

L = []
for i in range(laby.height):
    for j in range(laby.width):
        L.append((i,j))
print(f"Liste des cellules : \n{L}")
Liste des cellules : 
[(0, 0), (0, 1), (0, 2), (0, 3), (1, 0), (1, 1), (1, 2), (1, 3), (2, 0), (2, 1), (2, 2), (2, 3), (3, 0), (3, 1), (3, 2), (3, 3)]

Manipulation de labyrinthes​

Nous allons avoir besoin de méthodes d'instance essentielles, pour construire et résoudre ces problèmes de labyrinthes.

Construisons d'abord, à titre d'exemple, la méthode add_wall(c1, c2) qui ajoute un mur entre entre la cellule c1 et la cellule c2.

Ajouter un mur entre deux cellules revient à couper la possibilité de se déplacer de l'une à l'autre et inversement. Il s'agit donc de retirer c1 des voisines de c2, et de retirer c2 des voisines de c1.

Ce qui donne :

def add_wall(c1, c2):
    self.neighbors[c1].remove(c2)
    self.neighbors[c2].remove(c1)

Remarque : notez l'usage de self ; self désigne l'objet sur lequel sera appliquée la méthode ; on peut donc comprendre self.neighbors[c1].remove(c2)comme « retirer c2 des voisins de c1, dans la labyrinthe sur lequel la méthode add_wall(C&, c2) sera appliquée »

Version robuste

On aurait aussi pu vérifier que les cellules passées en paramètres ont des coordonnées cohérentes avec la grille, et que les cellules sont bien voisines l'une de l'autre :

def add_wall(self, c1, c2):
    # Facultatif : on teste si les sommets sont bien dans le labyrinthe
    assert 0 <= c1[0] < self.height and \
        0 <= c1[1] < self.width and \
        0 <= c2[0] < self.height and \
        0 <= c2[1] < self.width, \
        f"Erreur lors de l'ajout d'un mur entre {c1} et {c2} : les coordonnées de sont pas compatibles avec les dimensions du labyrinthe"
    # Ajout du mur
    if c2 in self.neighbors[c1]:      # Si c2 est dans les voisines de c1
        self.neighbors[c1].remove(c2) # on le retire
    if c1 in self.neighbors[c2]:      # Si c3 est dans les voisines de c2
        self.neighbors[c2].remove(c1) # on le retire

Exemple d'utilisation :

laby = Maze(1, 2)
print(laby)
┏━━━┳━━━┓
┃   ┃   ┃
┗━━━┻━━━┛
laby.neighbors[(0, 0)].add((0, 1))
laby.neighbors[(0, 1)].add((0, 0))
print(laby)
┏━━━┳━━━┓
┃       ┃
┗━━━┻━━━┛
laby.add_wall((0, 0), (0, 1))
print(laby)
┏━━━┳━━━┓
┃   ┃   ┃
┗━━━┻━━━┛
A faire

Écrire les méthodes d'instance suivantes :

  • remove_wall(c1, c2) qui supprime un mur entre deux cellules 🌶️
  • get_all_walls() qui retourne la liste de tous les murs sous la forme d'une liste de tuple de cellules 🌶️
  • get_contiguous_cells(c) qui retourne la liste des cellules contigües à c dans la grille (sans s'occuper des éventuels murs) 🌶️ 🌶️
  • get_reachable_cells(c) qui retourne la liste des cellules accessibles depuis c (c'est-à-dire les cellules contiguës à c qui sont dans le voisinage de c) 🌶️ 🌶️
Indications (cliquer pour voir)
  1. Pour simplifier l'écriture de ces méthodes, vous pourriez en écrire une qui retourne la liste de toutes les cellules de la grille du labyrinthe : get_all_cells().
- Soit L la liste des cellules (initialiser L à _vide_)
- Pour tout i allant de 0 à height-1:
    - Pour tout j allant de 0 à width-1:
        - Ajouter (i, j) à L
- Retourner L
  1. Un algorithme possible pour get_all_walls(c1) pourrait être :
- Soit L la liste des murs (initialiser L à _vide_)
- Pour chaque cellule c1 de la grille :
    - Si la cellule c2 à droite de c1 est dans la grille **et** qu'elle n'est pas dans les voisines de c1:
        - Ajouter le mur [c1, c2] à L
    - Si la cellule c3 en dessous de c1 est dans la grille **et** qu'elle n'est pas dans les voisines de c1:
        - Ajouter le mur [c1, c3] à L
- Retourner L
  1. Les cellules contiguës (retournées par get_contiguous(c1)) d'une cellule (i,j)(i,j) (notée c1 ici) sont les cellules :
  • (i−1,j)(i-1, j) si i−1>=0i-1 >= 0
  • (i+1,j)(i+1, j) si i+1<heighti+1 < \text{height}
  • (i,j−1)(i, j-1) si j−1>=0j-1 >= 0
  • (i,j+1)(i, j+1) si j+1<widthj+1 < \text{width}
  1. Les cellules atteignables (retournées par get_reachable(c1)) depuis une cellule (i,j)(i,j) (notée c1 ici) sont les cellules :
  • contiguës à (i,j)(i,j)
  • et qui ne sont pas séparées de (i,j)(i,j) par un mur

Exemple d'utilisation de ces méthodes :

laby = Maze(5, 5)
print(laby)
┏━━━┳━━━┳━━━┳━━━┳━━━┓
┃   ┃   ┃   ┃   ┃   ┃
┣━━━╋━━━╋━━━╋━━━╋━━━┫
┃   ┃   ┃   ┃   ┃   ┃
┣━━━╋━━━╋━━━╋━━━╋━━━┫
┃   ┃   ┃   ┃   ┃   ┃
┣━━━╋━━━╋━━━╋━━━╋━━━┫
┃   ┃   ┃   ┃   ┃   ┃
┣━━━╋━━━╋━━━╋━━━╋━━━┫
┃   ┃   ┃   ┃   ┃   ┃
┗━━━┻━━━┻━━━┻━━━┻━━━┛
laby.remove_wall((0, 0), (0, 1))
print(laby)
┏━━━┳━━━┳━━━┳━━━┳━━━┓
┃       ┃   ┃   ┃   ┃
┣━━━╋━━━╋━━━╋━━━╋━━━┫
┃   ┃   ┃   ┃   ┃   ┃
┣━━━╋━━━╋━━━╋━━━╋━━━┫
┃   ┃   ┃   ┃   ┃   ┃
┣━━━╋━━━╋━━━╋━━━╋━━━┫
┃   ┃   ┃   ┃   ┃   ┃
┣━━━╋━━━╋━━━╋━━━╋━━━┫
┃   ┃   ┃   ┃   ┃   ┃
┗━━━┻━━━┻━━━┻━━━┻━━━┛
laby.empty()
laby.add_wall((0, 0), (0, 1))
laby.add_wall((0, 1), (1, 1))
print(laby)
┏━━━┳━━━┳━━━┳━━━┳━━━┓
┃   ┃               ┃
┣   ╋━━━╋   ╋   ╋   ┫
┃                   ┃
┣   ╋   ╋   ╋   ╋   ┫
┃                   ┃
┣   ╋   ╋   ╋   ╋   ┫
┃                   ┃
┣   ╋   ╋   ╋   ╋   ┫
┃                   ┃
┗━━━┻━━━┻━━━┻━━━┻━━━┛
print(laby.get_all_walls())
[[(0, 0), (0, 1)], [(0, 1), (1, 1)]]
print(laby.get_contiguous_cells((0,1)))
[(1, 1), (0, 0), (0, 2)]
print(laby.get_reachable_cells((0,1)))
[(0, 2)]

Génération​

Nous allons maintenant nous intéresser aux algorithmes permettant de générer des labyrinthes parfaits.

Nous allons commencer par implémenter deux classiques assez simples, l'un reposant sur les arbres binaires et le second, appelé sidewinder. Nous verrons aussi deux algorithmes un peu plus avancés, qu'on retrouve notamment dans l'article wikipedia consacré à la modélisation mathématique des labyrinthes :

  • l'algorithme de génération par fusion de chemins (qui peut-être vu comme une forme de l'algorithme de Kruskal, qui permet de déterminer un arbre couvrant de poids minimal dans un graphe non-orienté valué)
  • l'algorithme de génération par exploration exhaustive (qui utilise un parcours de graphe, en profondeur ou en largeur)

On terminera par l'algorithme de Wilson.

Méthode de classe

Les méthodes de générations seront implémentées comme des méthodes de classe. Comme leur nom l'indique les méthodes de classes s'appliquent au nom de la classe (Maze) et pas à une instance (laby par exemple).

Pour définir une méthode de classe en python, il est nécessaire de faire précéder la définition de la méthode par le décorateur @classmethod, et à remplacer self par cls :

@classmethod
def ma_methode_de_classe(cls, param1, param2):
    #
    #
    #


ma_classe.ma_methode_de_classe(p1, p2)

Exemples :

laby = Maze.gen_btree(4, 4)
print(laby)
┏━━━┳━━━┳━━━┳━━━┓
┃   ┃       ┃   ┃
┣   ╋━━━╋   ╋   ┫
┃       ┃   ┃   ┃
┣━━━╋   ╋   ╋   ┫
┃   ┃           ┃
┣   ╋━━━╋━━━╋   ┫
┃               ┃
┗━━━┻━━━┻━━━┻━━━┛

Arbre binaire​

L'algorithme de génération par arbre binaire consiste à générer… un arbre binaire comme support du labyrinthe.

La procédure est assez simple :

Algorithme de construction par arbre binaire
  • Initialisation : un labyrinthe plein (contenant tous les murs possibles)
  • Pour chaque cellule du labyrinthe :
    • Supprimer aléatoirement le mur EST ou le mur SUD (s'il n'en possède qu'un, supprimer ce mur ; s'il n'en possède aucun des deux, ne rien faire)

Remarque : on utilisera dans la suite de ce document les points cardinaux (NORD, SUD, EST, OUEST) pour l'orientation sur la grille.

A faire

Écrire une méthode de classe gen_btree(h, w) qui génère un labyrinthe à hh lignes et ww colonnes, en utilisant l'algorithme de construction par arbre binaire. 🌶️🌶️🌶️

Sidewinder​

L'algorithme de génération sidewinder ressemble beaucoup au précédent. L'idée est de procéder ligne par ligne, d'OUEST en EST, en choisissant aléatoirement de casser le mur EST d'une cellule. Pour chaque séquence de cellules voisines (connectées) créée sur la ligne, on casse un mur SUD au hasard d'une de ces cellules (une séquence peut être constituée d'une seule cellule).

On pourrait formaliser le pseudo code de la façon suivante :

Algorithme sidewinder
  • Initialisation : création d'un labyrinthe plein
  • Pour i allant de 0 à hauteur-2 :
    • Initialiser une variable séquence comme liste vide
    • Pour j allant de 0 à largeur-2 :
      • Ajouter la cellule (i,j)(i, j) à la séquence
      • Tirer à pile ou face :
        • Si c'est pile : Casser le mur EST de la cellule (i,j)(i, j)
        • Si c'est face :
          • Casser le mur SUD d'une des cellules (choisie au hasard) qui constituent le séquence qui vient d'être terminée.
          • Réinitialiser la séquence à une liste vide
    • Ajouter la dernière cellule à la séquence
    • Tirer une cellule au sort dans la séquence et casser son mur SUD
  • Casser tous les murs EST de la dernière ligne
  • Retourner le labyrinthe
A faire

Écrire une méthode de classe gen_sidewinder(h, w) qui génère une labyrinthe à hh lignes et ww colonnes, en utilisant l'algorithme de construction sidewinder.🌶️🌶️🌶️

laby = Maze.gen_sidewinder(4, 4)
print(laby)
┏━━━┳━━━┳━━━┳━━━┓
┃       ┃   ┃   ┃
┣━━━╋   ╋   ╋   ┫
┃       ┃       ┃
┣━━━╋   ╋━━━╋   ┫
┃       ┃   ┃   ┃
┣━━━╋   ╋   ╋   ┫
┃               ┃
┗━━━┻━━━┻━━━┻━━━┛
Note

Si vous essayez les générateurs précédents plusieurs fois, vous devriez observer des patterns (au delà de la dernière ligne, qui est un défaut évident). Ces caractéristiques sont des défauts majeurs pour un labyrinthe.

Fusion de chemins​

L'algorithme de fusion de chemins consiste à partir d'un labyrinthe « plein », puis à casser des murs au hasard en évitant de créer des cycles. Puisqu'un labyrinthe parfait est un arbre, et qu'un arbre à sommets a exactement n−1n - 1 arêtes, il suffit d'abattre n−1n - 1 murs (soit h×w−1h \times w - 1 si hh et ww donnent respectivement le nombre de lignes et le nombre de colonnes).

Pour éviter de créer des cycles, on utilise un mécanisme de labélisation des cellules (avec des entiers). Lorsqu'on casse un mur depuis une cellule, le label de la cellule « se propage » dans la zone découverte. Mais on n'ouvrira un mur que lorsque le label de la cellule courante est différent du label de la cellule qui est de l'autre côté du mur.

Voici la description de l'algorithme :

Algorithme par fusion de chemins
  • Initialisation :
    • on remplit le labyrinthe avec tous les murs possibles
    • on labélise les cellules de 1 à nn
    • on extrait la liste de tous les murs et on les « mélange » (on les permute aléatoirement)
  • Pour chaque mur de la liste :
    • Si les deux cellules séparées par le mur n'ont pas le même label :
      • casser le mur
      • affecter le label de l'une des deux cellules, à l'autre, et à toutes celles qui ont le même label que la deuxième

Illustration animée issue de l'article wikipedia consacré à la modélisation mathématique des labyrinthes

A faire

Écrire une méthode de classe gen_fusion(h,w) qui génère un labyrinthe, à hh lignes et ww colonnes, parfait, avec l'algorithme de fusion de chemins. 🌶️🌶️🌶️

Exemple :

laby = Maze.gen_fusion(15,15)
print(laby)
┏━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┓
┃   ┃   ┃       ┃               ┃   ┃           ┃   ┃   ┃   ┃
┣   ╋   ╋━━━╋   ╋   ╋   ╋   ╋━━━╋   ╋━━━╋   ╋   ╋   ╋   ╋   ┫
┃       ┃           ┃   ┃           ┃       ┃   ┃           ┃
┣   ╋━━━╋   ╋━━━╋   ╋━━━╋━━━╋━━━╋   ╋   ╋   ╋━━━╋   ╋   ╋━━━┫
┃       ┃   ┃   ┃       ┃       ┃       ┃           ┃   ┃   ┃
┣   ╋━━━╋   ╋   ╋━━━╋   ╋   ╋   ╋━━━╋━━━╋   ╋━━━╋━━━╋   ╋   ┫
┃               ┃           ┃           ┃   ┃               ┃
┣━━━╋   ╋━━━╋━━━╋   ╋   ╋━━━╋   ╋━━━╋   ╋   ╋━━━╋   ╋━━━╋━━━┫
┃           ┃       ┃   ┃       ┃   ┃   ┃   ┃       ┃       ┃
┣   ╋━━━╋   ╋   ╋━━━╋━━━╋━━━╋━━━╋   ╋━━━╋   ╋━━━╋━━━╋━━━╋   ┫
┃   ┃       ┃                       ┃           ┃   ┃   ┃   ┃
┣   ╋━━━╋━━━╋━━━╋   ╋   ╋━━━╋━━━╋━━━╋   ╋━━━╋   ╋   ╋   ╋   ┫
┃               ┃   ┃   ┃           ┃       ┃               ┃
┣━━━╋   ╋   ╋━━━╋   ╋━━━╋   ╋━━━╋━━━╋━━━╋━━━╋━━━╋   ╋━━━╋   ┫
┃   ┃   ┃   ┃       ┃   ┃           ┃       ┃       ┃   ┃   ┃
┣   ╋   ╋   ╋━━━╋   ╋   ╋   ╋   ╋━━━╋   ╋   ╋━━━╋   ╋   ╋━━━┫
┃       ┃       ┃   ┃       ┃           ┃   ┃       ┃       ┃
┣━━━╋━━━╋   ╋━━━╋━━━╋━━━╋   ╋   ╋━━━╋━━━╋   ╋━━━╋   ╋   ╋   ┫
┃       ┃       ┃       ┃   ┃           ┃               ┃   ┃
┣   ╋   ╋━━━╋━━━╋   ╋   ╋━━━╋━━━╋━━━╋━━━╋   ╋━━━╋   ╋   ╋━━━┫
┃   ┃       ┃       ┃   ┃   ┃       ┃   ┃       ┃   ┃       ┃
┣   ╋━━━╋━━━╋   ╋━━━╋   ╋   ╋━━━╋   ╋   ╋━━━╋━━━╋━━━╋   ╋━━━┫
┃   ┃       ┃       ┃   ┃           ┃                       ┃
┣   ╋   ╋━━━╋   ╋   ╋━━━╋━━━╋   ╋━━━╋   ╋━━━╋━━━╋━━━╋━━━╋━━━┫
┃           ┃   ┃       ┃                   ┃               ┃
┣   ╋   ╋   ╋━━━╋   ╋   ╋━━━╋━━━╋━━━╋━━━╋   ╋   ╋   ╋━━━╋   ┫
┃   ┃   ┃   ┃       ┃               ┃       ┃   ┃   ┃       ┃
┣   ╋━━━╋   ╋   ╋   ╋━━━╋   ╋━━━╋━━━╋   ╋   ╋━━━╋━━━╋   ╋   ┫
┃   ┃           ┃       ┃               ┃               ┃   ┃
┗━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┛

Exploration exhaustive​

Une deuxième idée consiste à « explorer » aléatoirement le labyrinthe, à la manière d'un parcours en profondeur, en cassant les murs à mesure qu'on avance :

Algorithme de génération par exploration
  • Initialisation :
    • Choisir une cellule au hasard
    • Marquer cette cellule comme étant visitée
    • Mettre cette cellule dans sur une pile
  • Tant qu'il reste des cellules non-marquées :
    • Prendre la cellule en haut de la pile et l'en retirer
    • Si cette cellule a des voisins qui n'ont pas encore été visités :
      • La remettre sur la pile
      • Choisir au hasard l'une de ses cellules contigües qui n'a pas été visitée
      • Casser le mur entre la cellule (celle qui a été dépilée) et celle qui vient d'être choisie
      • Marquer la cellule qui vient d'être choisie comme visitée
      • Et la mettre sur la pile

Illustration animée issue de l'article wikipedia consacré à la modélisation mathématique des labyrinthes

A faire

Écrire une méthode de classe gen_exploration(h,w) qui génère un labyrinthe, à hh lignes et ww colonnes, parfait, avec l'algorithme d'exploration exhaustive. 🌶️🌶️🌶️

Exemple :

laby = Maze.gen_exploration(15,15)
print(laby)
┏━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┓
┃               ┃                                   ┃       ┃
┣   ╋━━━╋━━━╋   ╋   ╋━━━╋━━━╋   ╋━━━╋━━━╋━━━╋━━━╋   ╋━━━╋   ┫
┃   ┃       ┃   ┃   ┃       ┃           ┃   ┃       ┃       ┃
┣   ╋   ╋   ╋   ╋━━━╋   ╋   ╋━━━╋   ╋   ╋   ╋   ╋━━━╋   ╋   ┫
┃   ┃   ┃   ┃   ┃       ┃       ┃   ┃   ┃               ┃   ┃
┣   ╋━━━╋   ╋   ╋   ╋━━━╋━━━╋   ╋━━━╋   ╋━━━╋━━━╋━━━╋━━━╋   ┫
┃       ┃   ┃       ┃       ┃       ┃               ┃   ┃   ┃
┣   ╋   ╋   ╋━━━╋━━━╋   ╋━━━╋━━━╋   ╋   ╋━━━╋━━━╋   ╋   ╋   ┫
┃   ┃   ┃           ┃           ┃   ┃       ┃       ┃       ┃
┣━━━╋   ╋   ╋   ╋   ╋━━━╋   ╋   ╋   ╋━━━╋━━━╋   ╋━━━╋   ╋━━━┫
┃       ┃   ┃   ┃           ┃   ┃   ┃           ┃   ┃   ┃   ┃
┣   ╋━━━╋   ╋   ╋━━━╋━━━╋━━━╋━━━╋   ╋   ╋━━━╋━━━╋   ╋   ╋   ┫
┃   ┃       ┃                   ┃       ┃   ┃       ┃       ┃
┣   ╋   ╋━━━╋━━━╋━━━╋━━━╋━━━╋   ╋━━━╋━━━╋   ╋   ╋   ╋━━━╋   ┫
┃   ┃           ┃           ┃   ┃               ┃           ┃
┣   ╋━━━╋━━━╋   ╋   ╋━━━╋━━━╋   ╋   ╋━━━╋━━━╋━━━╋━━━╋━━━╋━━━┫
┃   ┃               ┃       ┃   ┃   ┃       ┃               ┃
┣   ╋━━━╋━━━╋━━━╋   ╋   ╋   ╋   ╋   ╋   ╋   ╋━━━╋━━━╋━━━╋   ┫
┃           ┃       ┃   ┃       ┃       ┃                   ┃
┣━━━╋━━━╋   ╋━━━╋━━━╋   ╋━━━╋━━━╋━━━╋━━━╋━━━╋━━━╋━━━╋━━━╋   ┫
┃       ┃           ┃                           ┃       ┃   ┃
┣   ╋━━━╋━━━╋━━━╋   ╋   ╋━━━╋━━━╋   ╋━━━╋━━━╋━━━╋   ╋   ╋   ┫
┃       ┃           ┃           ┃                   ┃   ┃   ┃
┣   ╋   ╋   ╋━━━╋━━━╋━━━╋━━━╋   ╋━━━╋━━━╋━━━╋━━━╋━━━╋   ╋   ┫
┃   ┃   ┃       ┃   ┃       ┃   ┃           ┃       ┃   ┃   ┃
┣━━━╋   ╋━━━╋   ╋   ╋   ╋   ╋   ╋━━━╋   ╋   ╋   ╋━━━╋   ╋   ┫
┃           ┃       ┃   ┃   ┃       ┃   ┃   ┃   ┃       ┃   ┃
┣   ╋━━━╋━━━╋━━━╋━━━╋   ╋   ╋━━━╋   ╋   ╋   ╋   ╋   ╋━━━╋   ┫
┃                       ┃               ┃       ┃           ┃
┗━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┛

L'algorithme de Wilson​

Terminons avec un algorithme plus amusant, qui donne des labyrinthes très intéressants : l'algorithme de Wilson. Il repose sur les marches aléatoires.

L'idée est la suivante : on va construire le labyrinthe en essayant des chemins aléatoires, jusqu'à obtention d'une arborescence…

Algorithme de Wilson
  • Choisir une cellule au hasard sur la grille et la marquer
  • Tant qu'il reste des cellules non marquées :
    • Choisir une cellule de départ au hasard, parmi les cellules non marquées
    • Effectuer une marche aléatoire jusqu'à ce qu'une cellule marquée soit atteinte (en cas de boucle, si la tête du snake se mord la queue, « couper » la boucle formée [autrement dit, supprimer toutes étapes depuis le précédent passage])
    • Marquer chaque cellule du chemin, et casser tous les murs rencontrés, jusqu'à la cellule marquée
A faire

Écrire une méthode de classe gen_wilson(h, w) qui implémente cet algorithme. 🌶️🌶️🌶️🌶️🌶️

Exemple :

laby = Maze.gen_wilson(12, 12)
print(laby)
┏━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┓
┃   ┃       ┃   ┃   ┃                           ┃
┣   ╋   ╋   ╋   ╋   ╋   ╋━━━╋   ╋━━━╋━━━╋   ╋━━━┫
┃       ┃               ┃       ┃   ┃       ┃   ┃
┣   ╋━━━╋   ╋━━━╋━━━╋   ╋━━━╋━━━╋   ╋━━━╋━━━╋   ┫
┃       ┃   ┃   ┃   ┃           ┃       ┃       ┃
┣   ╋   ╋━━━╋   ╋   ╋━━━╋━━━╋   ╋   ╋━━━╋━━━╋   ┫
┃   ┃           ┃   ┃           ┃   ┃       ┃   ┃
┣   ╋━━━╋━━━╋   ╋   ╋━━━╋━━━╋   ╋   ╋   ╋━━━╋   ┫
┃       ┃   ┃           ┃                   ┃   ┃
┣━━━╋   ╋   ╋━━━╋   ╋━━━╋   ╋   ╋   ╋━━━╋   ╋   ┫
┃   ┃   ┃           ┃       ┃   ┃       ┃       ┃
┣   ╋   ╋━━━╋   ╋   ╋━━━╋━━━╋━━━╋━━━╋━━━╋━━━╋   ┫
┃           ┃   ┃                   ┃           ┃
┣━━━╋   ╋━━━╋━━━╋   ╋   ╋━━━╋━━━╋━━━╋━━━╋   ╋   ┫
┃           ┃       ┃                   ┃   ┃   ┃
┣   ╋━━━╋   ╋━━━╋━━━╋━━━╋━━━╋   ╋   ╋━━━╋   ╋   ┫
┃   ┃           ┃               ┃   ┃       ┃   ┃
┣   ╋   ╋━━━╋━━━╋   ╋━━━╋   ╋━━━╋━━━╋━━━╋   ╋━━━┫
┃   ┃   ┃               ┃       ┃   ┃   ┃   ┃   ┃
┣━━━╋━━━╋   ╋   ╋━━━╋   ╋   ╋━━━╋   ╋   ╋━━━╋   ┫
┃           ┃   ┃   ┃   ┃                       ┃
┣━━━╋━━━╋   ╋━━━╋   ╋━━━╋   ╋━━━╋━━━╋   ╋   ╋━━━┫
┃                       ┃           ┃   ┃       ┃
┗━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┛

Résolution​

Avant d'écrire des méthodes de résolution de labyrinthe, ajoutez cette méthode à votre classe Maze :

def overlay(self, content=None):
    """
    Rendu en mode texte, sur la sortie standard, \
    d'un labyrinthe avec du contenu dans les cellules
    Argument:
        content (dict) : dictionnaire tq content[cell] contient le caractère à afficher au milieu de la cellule
    Retour:
        string
    """
    if content is None:
        content = {(i,j):' ' for i in range(self.height) for j in range(self.width)}
    else:
        # Python >=3.9
        #content = content | {(i, j): ' ' for i in range(
        #    self.height) for j in range(self.width) if (i,j) not in content}
        # Python <3.9
        new_content = {(i, j): ' ' for i in range(self.height) for j in range(self.width) if (i,j) not in content}
        content = {**content, **new_content}
    txt = r""
    # Première ligne
    txt += "┏"
    for j in range(self.width-1):
        txt += "━━━┳"
    txt += "━━━┓\n"
    txt += "┃"
    for j in range(self.width-1):
        txt += " "+content[(0,j)]+" ┃" if (0,j+1) not in self.neighbors[(0,j)] else " "+content[(0,j)]+"  "
    txt += " "+content[(0,self.width-1)]+" ┃\n"
    # Lignes normales
    for i in range(self.height-1):
        txt += "┣"
        for j in range(self.width-1):
            txt += "━━━╋" if (i+1,j) not in self.neighbors[(i,j)] else "   ╋"
        txt += "━━━┫\n" if (i+1,self.width-1) not in self.neighbors[(i,self.width-1)] else "   ┫\n"
        txt += "┃"
        for j in range(self.width):
            txt += " "+content[(i+1,j)]+" ┃" if (i+1,j+1) not in self.neighbors[(i+1,j)] else " "+content[(i+1,j)]+"  "
        txt += "\n"
    # Bas du tableau
    txt += "┗"
    for i in range(self.width-1):
        txt += "━━━┻"
    txt += "━━━┛\n"
    return txt

Cette méthode permettra d'afficher un labyrinthe en mode texte en lui ajoutant des caractères dans les cellules (afin de visualiser les solutions trouvées, par exemple). Il suffit pour ça de fournir à overlay un dictionnaire content dont les clés sont des cellules et les valeurs sont les caractères à afficher dans les cellules correspondantes.

Exemples :

laby = Maze(4,4)
laby.empty()
print(laby.overlay({
    (0, 0):'c',
    (0, 1):'o',
    (1, 1):'u',
    (2, 1):'c',
    (2, 2):'o',
    (3, 2):'u',
    (3, 3):'!'}))
┏━━━┳━━━┳━━━┳━━━┓
┃ c   o         ┃
┣   ╋   ╋   ╋   ┫
┃     u         ┃
┣   ╋   ╋   ╋   ┫
┃     c   o     ┃
┣   ╋   ╋   ╋   ┫
┃         u   ! ┃
┗━━━┻━━━┻━━━┻━━━┛
laby = Maze(4,4)
laby.empty()
path = {(0, 0): '@',
        (1, 0): '*',
        (1, 1): '*',
        (2, 1): '*',
        (2, 2): '*',
        (3, 2): '*',
        (3, 3): '§'}
print(laby.overlay(path))
┏━━━┳━━━┳━━━┳━━━┓
┃ @             ┃
┣   ╋   ╋   ╋   ┫
┃ *   *         ┃
┣   ╋   ╋   ╋   ┫
┃     *   *     ┃
┣   ╋   ╋   ╋   ┫
┃         *   § ┃
┗━━━┻━━━┻━━━┻━━━┛

Résolution par parcours​

L'algorithme le plus évident pour résoudre un problème de labyrinthe, consiste à adapter le parcours « en profondeur d'abord » de l'arborescence associée au labyrinthe :

Algorithme de résolution par parcours (pour aller de la cellule D à la cellule A)

Parcours du graphe jusqu'à ce qu'on trouve A

  • Initialisation :
    • Placer D dans la struture d'attente (file ou pile) et marquer D
    • Mémoriser l'élément prédécesseur de D comme étant D
  • Tant qu'il reste des cellules non-marquées :
    • Prendre la « première » cellule et la retirer de la structure (appelons c, cette cellule)
    • Si c correspond à A :
      • C'est terminé, on a trouvé un chemin vers la cellule de destination
    • Sinon :
      • Pour chaque voisin de c :
        • Si elle n'est pas marquée :
          • La marquer
          • La mettre dans la structure d'attente
          • Mémoriser son prédécesseur comme étant c

Reconstruction du chemin à partir des prédécesseurs

  • Initialier c à A
  • Tant que c n'est pas D :
    • ajouter c au chemin
    • mettre le prédécesseur de c dans c
  • Ajouter D au chemin

Retourner le chemin

A faire

Implémenter cet algorithme dans une méthode d'instance solve_dfs(start, stop) 🌶️🌶️🌶️ qui prend la cellule de départ et la cellule d'arrivée comme arguments. Créer ensuite une méthode solve_bfs(start, stop) 🌶️🌶️🌶️ qui implémente cette fois un parcours en largeur🌶️🌶️🌶️

Indications/rappels
  • Si vous choisissez une file comme structure d'attente, il s'agit du parcours en largeur ; si vous prenez une pile, il s'agit d'un parcours en profondeur.
  • Un chemin est simplement une succession de cellules. On pourra la représenter avec une liste (ou un tuple), constituée des tuples des cellules.
  • Pour mémoriser les prédécesseurs, on utilisera un dictionnaire pred dont chaque clé est une cellule et chaque valeur également.

Exemples :

laby = Maze.gen_fusion(15, 15)
solution = laby.solve_dfs((0, 0), (14, 14))
str_solution = {c:'*' for c in solution}
str_solution[( 0,  0)] = 'D'
str_solution[(14, 14)] = 'A'
print(laby.overlay(str_solution))
┏━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┓
┃ D     ┃   ┃               ┃       ┃   ┃       ┃           ┃
┣   ╋━━━╋   ╋━━━╋━━━╋   ╋━━━╋   ╋━━━╋   ╋━━━╋   ╋   ╋━━━╋━━━┫
┃ * ┃                       ┃   ┃                   ┃       ┃
┣   ╋   ╋━━━╋   ╋━━━╋━━━╋━━━╋   ╋━━━╋   ╋━━━╋━━━╋━━━╋   ╋━━━┫
┃ *     ┃   ┃   ┃           ┃               ┃               ┃
┣   ╋━━━╋   ╋━━━╋━━━╋━━━╋   ╋━━━╋━━━╋   ╋   ╋   ╋━━━╋   ╋━━━┫
┃ *   *   *   *   *   *   *     ┃ *   * ┃   ┃   ┃       ┃   ┃
┣━━━╋━━━╋   ╋━━━╋━━━╋   ╋   ╋━━━╋   ╋   ╋━━━╋   ╋   ╋   ╋   ┫
┃               ┃   ┃   ┃ *   *   * ┃ * ┃   ┃   ┃   ┃       ┃
┣   ╋   ╋   ╋   ╋   ╋━━━╋━━━╋━━━╋   ╋   ╋   ╋   ╋━━━╋   ╋━━━┫
┃   ┃   ┃   ┃       ┃           ┃   ┃ *     ┃   ┃       ┃   ┃
┣   ╋━━━╋━━━╋   ╋━━━╋   ╋   ╋   ╋   ╋   ╋━━━╋━━━╋━━━╋   ╋   ┫
┃           ┃   ┃       ┃   ┃   ┃   ┃ * ┃   ┃           ┃   ┃
┣━━━╋   ╋━━━╋━━━╋   ╋   ╋   ╋━━━╋   ╋   ╋   ╋━━━╋   ╋   ╋   ┫
┃           ┃   ┃   ┃   ┃       ┃   ┃ *     ┃       ┃   ┃   ┃
┣   ╋━━━╋━━━╋   ╋━━━╋   ╋━━━╋━━━╋━━━╋   ╋━━━╋   ╋━━━╋━━━╋   ┫
┃       ┃   ┃       ┃           ┃ *   * ┃                   ┃
┣   ╋   ╋   ╋   ╋━━━╋━━━╋   ╋━━━╋   ╋━━━╋━━━╋━━━╋   ╋━━━╋━━━┫
┃   ┃           ┃   ┃             *     ┃   ┃               ┃
┣   ╋━━━╋   ╋   ╋   ╋   ╋   ╋   ╋   ╋━━━╋   ╋   ╋━━━╋━━━╋━━━┫
┃       ┃   ┃   ┃       ┃   ┃   ┃ *     ┃             *   * ┃
┣   ╋━━━╋   ╋━━━╋━━━╋   ╋   ╋━━━╋   ╋━━━╋━━━╋   ╋   ╋   ╋   ┫
┃       ┃           ┃   ┃   ┃     *     ┃   ┃   ┃   ┃ * ┃ * ┃
┣━━━╋   ╋   ╋━━━╋   ╋   ╋   ╋   ╋   ╋━━━╋   ╋   ╋   ╋   ╋   ┫
┃       ┃       ┃   ┃   ┃   ┃   ┃ *   * ┃       ┃   ┃ * ┃ * ┃
┣━━━╋━━━╋━━━╋   ╋━━━╋   ╋━━━╋━━━╋━━━╋   ╋━━━╋   ╋━━━╋   ╋   ┫
┃                   ┃       ┃         * ┃       ┃     * ┃ * ┃
┣   ╋   ╋   ╋   ╋   ╋   ╋━━━╋━━━╋━━━╋   ╋━━━╋━━━╋━━━╋   ╋   ┫
┃   ┃   ┃   ┃   ┃   ┃   ┃             *   *   *   *   * ┃ A ┃
┗━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┛
laby = Maze.gen_exploration(15, 15)
solution = laby.solve_bfs((0, 0), (14, 14))
str_solution = {c:'*' for c in solution}
str_solution[( 0,  0)] = 'D'
str_solution[(14, 14)] = 'A'
print(laby.overlay(str_solution))
┏━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┳━━━┓
┃ D   *   *   *   *         ┃ *   *     ┃ *   * ┃ *   *   * ┃
┣   ╋━━━╋━━━╋━━━╋   ╋   ╋━━━╋   ╋   ╋━━━╋   ╋   ╋   ╋━━━╋   ┫
┃   ┃ *   *   *   * ┃   ┃ *   * ┃ *   *   * ┃ *   *     ┃ * ┃
┣   ╋   ╋━━━╋━━━╋━━━╋   ╋   ╋━━━╋━━━╋━━━╋━━━╋━━━╋━━━╋━━━╋   ┫
┃   ┃ *   *   *   * ┃   ┃ *   *   * ┃     *   * ┃ *   *   * ┃
┣   ╋━━━╋━━━╋━━━╋   ╋━━━╋━━━╋━━━╋   ╋   ╋   ╋   ╋   ╋━━━╋   ┫
┃       ┃       ┃ *   *   *   * ┃ * ┃   ┃ * ┃ * ┃ *   * ┃   ┃
┣━━━╋   ╋   ╋   ╋━━━╋━━━╋━━━╋   ╋   ╋━━━╋   ╋   ╋━━━╋   ╋━━━┫
┃   ┃       ┃           ┃ *   * ┃ *   *   * ┃ *     ┃ *   * ┃
┣   ╋━━━╋━━━╋━━━╋━━━╋   ╋   ╋   ╋━━━╋━━━╋━━━╋   ╋━━━╋━━━╋   ┫
┃               ┃   ┃   ┃ * ┃               ┃ * ┃ *   * ┃ * ┃
┣━━━╋━━━╋   ╋   ╋   ╋   ╋   ╋━━━╋━━━╋━━━╋━━━╋   ╋   ╋   ╋   ┫
┃           ┃       ┃   ┃ *   *   *   *   *   * ┃ * ┃ * ┃ * ┃
┣   ╋   ╋━━━╋━━━╋━━━╋   ╋━━━╋━━━╋━━━╋━━━╋━━━╋━━━╋   ╋   ╋   ┫
┃   ┃   ┃               ┃ *   *   *   *   * ┃ *   * ┃ * ┃ * ┃
┣   ╋━━━╋   ╋━━━╋━━━╋━━━╋   ╋━━━╋━━━╋━━━╋   ╋   ╋━━━╋   ╋   ┫
┃   ┃       ┃           ┃ *   *   *   * ┃ *   * ┃     *   * ┃
┣   ╋   ╋━━━╋   ╋━━━╋   ╋━━━╋━━━╋━━━╋   ╋━━━╋━━━╋━━━╋━━━╋   ┫
┃   ┃       ┃   ┃       ┃           ┃ * ┃ *   *   * ┃       ┃
┣   ╋━━━╋   ╋   ╋   ╋━━━╋   ╋   ╋   ╋   ╋   ╋━━━╋   ╋   ╋━━━┫
┃       ┃       ┃       ┃   ┃   ┃   ┃ *   * ┃ *   * ┃       ┃
┣━━━╋   ╋━━━╋━━━╋━━━╋   ╋━━━╋   ╋   ╋━━━╋━━━╋   ╋━━━╋━━━╋   ┫
┃                   ┃           ┃   ┃   ┃ *   * ┃ *   * ┃   ┃
┣   ╋━━━╋━━━╋   ╋━━━╋━━━╋━━━╋━━━╋   ╋   ╋   ╋   ╋   ╋   ╋━━━┫
┃   ┃           ┃               ┃       ┃ * ┃   ┃ * ┃ *   * ┃
┣   ╋━━━╋━━━╋   ╋   ╋━━━╋━━━╋   ╋━━━╋   ╋   ╋━━━╋   ╋━━━╋   ┫
┃   ┃       ┃   ┃       ┃   ┃       ┃   ┃ *   *   * ┃     * ┃
┣   ╋   ╋   ╋━━━╋━━━╋   ╋   ╋   ╋━━━╋   ╋━━━╋━━━╋━━━╋   ╋   ┫
┃       ┃                   ┃           ┃               ┃ A ┃
┗━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┻━━━┛

Résolution en aveugle : « la main droite »​

L'algorithme, bien connu, dit « de la main droite » peut-être vu comme une recherche « en profondeur d'abord » mais sans vision globale du labyrinthe. C'est la situation dans laquelle serait un individu qu'on abandonnerait dans un labyrinthe et qui devrait trouver la sortie. Il consiste à longer les murs en ayant toujours un contact avec un mur sur notre droite.

A faire

Implémenter cet algorithme dans une méthode d'instance solve_rhr(start, stop) qui retourne le chemin trouvé pour aller de start à stop. 🌶️🌶️🌶️🌶️🌶️

Évaluation​

Nous sommes désormais capables de générer des labyrinthes parfaits, et de les résoudre.

Il nous faudrait maintenant quelques outils d'évaluation des labyrinthes produits :

  • le labyrinthe généré est-il « facile » ?
  • la meilleure solution est-elle longue à trouver (relativement aux points de départ et d'arrivée) ?
A faire

Écrire une méthode d'instance distance_geo(c1, c2) qui calcule la distance « géodésique » entre la cellule c1 et la cellule c2 (vous pourrez utiliser une des méthodes de résolution implémentées avant), c'est à dire le nombre minimal de déplacements nécessaires sur le graphe pour aller de c1 à c2.🌶️

Écrire une méthode d'instance distance_man(c1, c2) qui calcule la distance de Manhattan, h sur la grille, entre la cellule c1 et la cellule c2, c'est à dire le nombre minimal de déplacements nécessaires pour aller de c2 à c1 si le labyrinthe était vide de tout mur.🌶️

Écrire une méthode d'instance worst_path_len() qui retourne la longueur du plus long chemin menant du départ à une impasse (une feuille).🌶️🌶️

Écrire une méthode d'instance dead_end_number() qui retourne le nombre de culs-de-sacs présents dans le labyrinthe.🌶️🌶️

Du problème algorithmique au rogue like​

Dans cette partie vous allez utiliser votre classe Maze pour en faire un petit jeu de type rogue-like.

Concept​

L'idée du jeu est d'incarner un personnage qui doit se déplacer, en un minimum de temps (et/ou de coups) dans un labyrinthe et atteindre un ou plusieurs objectifs (ramasser un ensemble de trucs, atteindre un point particulier du labyrinthe, etc.) Des items pourront être disséminés dans le labyrinthe.

Les items n'ont de limite que votre imagination. En voici quelques exemples :

  • faille aléatoire : lorsque le personnage passe sur cet item, il est téléporté n'importe où dans le labyrinthe,
  • shuffle : cet item re-génère un labyrinthe, sans changer la position du joueur ni celle de l'objectif,
  • marteau : cet item permet de casser les murs autour de la cellule,
  • carte magique : grâce à cet item le joueur voit les premières étapes à suivre pour atteindre l'objectif (ou l'objectif le plus proche s'il y en a plusieurs),
  • …

Le niveau de difficulté sera croissant à mesure que le joueur gagne.

Interface​

Plusieurs choix s'offrent à vous, parmis lesquels :

  • rester dans le style poétiquement désuet de l'interface textuelle (en ASCII) ; dans ce cas, vous pourrez avoir besoin de quelques astuces :
    • les séquences d'échappement ANSI, qui permettent de positionner le curseur dans le terminal, effacer le terminal, ajouter des effets de couleur…
    • le module getkey qui permet les interactions avec le clavier
  • opter pour une interface graphique avec pygame
  • choisir un framework comme pyxel
  • …