Entiers positifs dans les bases 2, 10 et 16

info

📈 Objectifs du cours

• Savoir convertir un entier entre les bases 2, 10 et 16.

---

Représentation des entiers positifs

Le système décimal (base 10)

En effet, tout le monde sait compter en base 10 (décimal). Mais comment ça marche ? Comment est construit notre système ? Pour répondre à cette question à l'apparence simple, oubliez tout et reprenons depuis le début : comment avez-vous appris à compter à l'école ?

On peut penser que la base 10 vient du fait qu'on a 10 doigts (c'est possible mais pas sûr), mais en tout cas deux choses sont certaines :

• Il y a 10 chiffres : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
• Avec ces derniers, on peut compter jusqu'à 9.

Et si l'on veut aller au-delà de 9, il faut changer de rang.

Cela signifie que si le rang des unités est plein, il faut passer à celui des dizaines, puis des centaines, milliers et j'en passe.

Par exemple, le nombre 1234 se décompose comme suit :

4 unités, 3 dizaines, 2 centaines et 1 millier.

On peut alors l'écrire comme suit :

$$\begin{aligned} 1234 &= 1000 + 200 + 30 + 4 \\ 1234 &= 1 \times 10^3 + 2 \times 10^2 + 3 \times 10^1 + 4 \times 10^0 \end{aligned}$$

Le système binaire (base 2)

• Le système binaire est la base la plus simple.
• Il utilise donc seulement deux chiffres, 0 et 1, appelés bits (contraction de l'anglais binary digit).
• 8 bits forment un octet, qui peut représenter 256 valeurs différentes (de 0 à 255).
• Avec $n$ bits, on peut représenter $2^n$ valeurs différentes (de 0 à $2^n - 1$).

Utilisations

• Système de comptage des ordinateurs.
• Représentation du fonctionnement de l'électronique numérique (0 = éteint, 1 = allumé).
• Représentation de la vérité d'une proposition logique (0 = faux, 1 = vrai).

Le système hexadécimal (base 16)

• Le système hexadécimal est un système de numération en base 16.
• Il utilise donc 16 chiffres, 0 à 9 et A à F.
• Plus court que le binaire, mais plus long que le décimal.

Base 10	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Base 16	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

Utilisations

• Encodage des couleurs en informatique (ex : #FF5733).
• Représentation des adresses mémoire (ex : 0x1A3F).
• Utilisé dans les langages de programmation pour représenter des valeurs binaires de manière plus lisible.

📊 Méthode de conversion

♻️ Décimal ➜ Binaire / Hexa : division par la base

On divise régulièrement par la base, en prenant les restes. On concatène ensuite les restes (du dernier au premier) pour obtenir la représentation binaire de la valeur.

Exemple : 44 en binaire

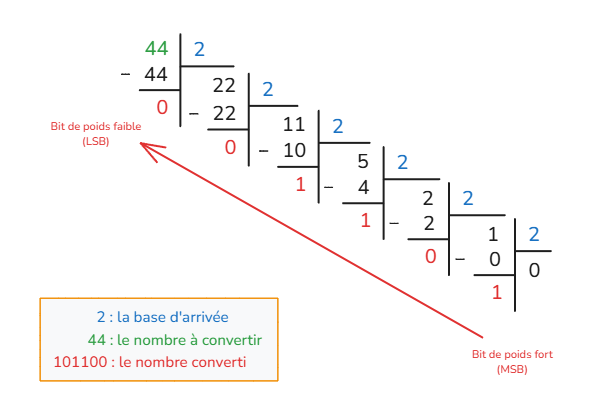
Le premier bit (le plus à gauche) est le bit de poids fort et le denrier (le plus à droite) est le bit de poids faible.

Exemple : 44 en hexadécimal

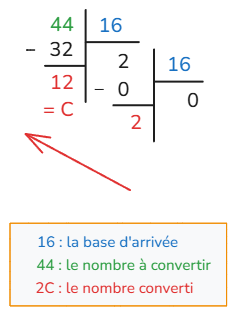
♻️ Binaire / Hexa ➜ Décimal : multiplication positionnelle

Exemple : $101100_2$

$$\begin{aligned} &= \textcolor{red}{1} \times 2^5 + \textcolor{red}{0} \times 2^4 + \textcolor{red}{1} \times 2^3 + \textcolor{red}{1} \times 2^2 + \textcolor{red}{0} \times 2^1 + \textcolor{red}{0} \times 2^0 \\ &= 32 + 0 + 8 + 4 + 0 + 0 = 44_{10} \end{aligned}$$

Exemple : $2C_{16}$

C se traduit par 12 en décimal

$$\begin{aligned} &= \textcolor{red}{2} \times 16^1 + \textcolor{red}{12} \times 16^0 \\ &= 32 + 12 = 44_{10} \end{aligned}$$

---

🔬 Astuce entre binaire et hexadécimal

1 chiffre hexa = 4 bits (car $2^4 = 16$)
Exemple :

Binaire	Hexa
0000	0
0001	1
1010	A
1111	F

Pour convertir rapidement :

• Groupes de 4 bits ➜ 1 chiffre hexa
• Inversement, chaque hexa ➜ 4 bits

---

💪 Entraînement interactif

Convertis 31₁₀ vers la base binaire

Convertis 79₁₀ vers la base hexadécimale

Convertis 1010000₂ vers la base décimale

Convertis 5E₁₆ vers la base décimale

---

📖 Entraînement

QCM

Les entiers positifs écrits en base 2 et qui se terminent par un 0 sont tous ...

Combien de nombres entiers différents peut-on coder avec 32 bits ?

Exercice 1

Produis la table de conversion de base 10 vers base 2 pour les entiers de 1 à 15.

Exercice 2

Combien de bits sont nécéssaires pour représenter les nombres suivants en binaire ?
⚠️ Je ne demande pas la conversion de ces nombres

• $256_{10}$
• $10_{10}$
• $485_{10}$
• $2028_{10}$
• $1023_{10}$

Et pour les représenter en hexadécimal ?

Supplément Python

Complête la fonction suivante afin qu'elle convertisse un entier positif en binaire sans utiliser la fonction bin().

def int_to_binary(n: int) -> str:
    if n == 0:
        return ...
    binary = ""
    while n > 0:
        binary = ...
        n = ...
    return binary

Ecris une nouvelle fonction qui convertit un entier positif en hexadécimal sans utiliser la fonction hex().

def int_to_hex(n: int) -> str:
    if n == 0:
        return ...
    hexa = "" 
    hex_chars = "0123456789ABCDEF"
    while n > 0:
        remainder = ...
        hexa = ...
        n = ...
    return hexa

Pour aller plus loin

• Ecrire un programme qui convertit un entier en binaire et en hexadécimal.
• Ecire une fonction qui convertir un entier en octal (base 8).